안녕하세요 밥한그릇 입니다. ^^
무더운 여름인데 다들 잘 지내고 계시나요? 저는 저번 주 수요일을 마지막으로 1학기가 종강한 상태입니다.
막 종강을 하고 방학을 맞이하게 된 대학생의 심정이란... 후련하면서도 마음 한구석이 허무하네요. (ㅠㅠ)
지난 학기에 데이터사이언스라는 과목을 수강했었는데, 무시무시한 과제량과 진도 분량 때문에 정말 너무 힘들었어요. 그렇지만 힘들었던 만큼 배운 내용이 많았기에, 잊어버리기 전에 한번 중요한 내용들을 리뷰해보려해요!
마지막 보강주차에 내용기반(content based) 검색 중 tf-idf 기반 문서 검색에 대해 배우게 되었어요.
그러니 이번 포스팅에서는 문서 검색의 원리와 tf-idf 문서 유사도(코사인 유사도) 계산법에 대해 알아보는 시간을 가지려 합니다.
그럼 시작합니다~
🔎 문서 검색
우리는 우리가 원하는 정보(문서)를 찾을 때, 주로 구글이나 네이버 같은 검색엔진을 많이 사용하죠. 이 검색 엔진의 원리는 대체 무엇일까요? 우리가 검색한 내용과 연관성이 높은 문서들을 어떻게 찾아주는 것일까요?
바로, 검색한 내용과 가장 관련성이 높은(또는 유사한) 순서대로 문서 목록을 생성해주면 됩니다. 그리고 관련성이 높은 것들부터 사용자에게 보여주면 끝나는 거에요.
그럼 문서의 순위는 어떻게 정할까요? 대상 집합에 포함된 각 문서에 관련도(유사성) 점수를 부여하면 됩니다.
이 유사성 점수를 부여하는 방법에는 자카드 계수와 단어 가방 모델(tf, df, idf ...) 등이 있습니다.
참고로 자카드 유사도의 계산에 대한 내용은 아래 더보기를 눌러보세요. 이번 포스팅에서는 단어가방 모델에서의 유사도 계산이 메인이므로 그것 위주로 설명하겠습니다.
두 문서의 자카드 유사도는 |교집합| / |합집합|으로 구할 수 있습니다.
구글에 "흥부와 놀부"를 검색했다고 해봅시다.
1. 다음의 두 문서가 나옵니다. 둘 중 어느 문서가 내 질의와 더 유사할까요?
문서 1 : 흥부와 놀부는 형제다
문서 2 : 흥부는 착하다
2. 질의와 문서들을 각각 용어 집합으로 변환해보아야겠네요.
질의 : {흥부, 놀부}
문서 1 : {흥부, 놀부, 형제}
문서 2 : {흥부, 착하다}
3. 자카드 계수로 계산해봅시다.
질의-문서1 : |{흥부, 놀부}| / |{흥부, 놀부, 형제}|
질의-문서1 : |{흥부}| / |{흥부, 놀부, 착하다}|
| { } | 는 해당 집합 안에 있는 원소의 개수를 의미합니다.
따라서 첫번째 식의 유사도는 2/3, 두번째 식의 유사도는 1/3이죠.
그러니 내 질의는 문서 1과의 유사도가 문서 2보다 더 높다고 볼 수 있겠습니다.
💼 단어가방 모델
자카드 유사도는 출현 여부(단어가 나오는 지/아닌 지)만 고려하고, 그 빈도수(단어가 몇 번 나오는 지)는 고려하지 않는다는 한계가 있습니다. 단어의 빈도수는 문서의 관련성에 큰 영향을 미치거든요. 드물게 출현하는 용어가 자주 출현하는 용어보다 많은 정보를 가지기 때문입니다. (informative)
그래서 단어의 빈도수를 유사도에 반영하기 위해, 이 단어 가방 모델이라는 것을 사용할 수 있습니다.
여기에서는 문서를 쪼개서 거기 나오는 단어의 빈도수를 표현하거나(tf), 어떤 단어가 출현하는 문서의 개수를 세거나(df) 해서 이를 벡터로 표현합니다.
말이 어렵죠? 아래의 예시를 보고 이해해봅시다.
참고로, 아래의 예시에서는 소숫점 3번째 자리에서 값을 반올림하여 나타냅니다.
✍ tf와 idf 예제
1) 다음의 문서 3개를 tf(단어 빈도수 벡터)와 df(문서 빈도수 벡터)로 나타내 봅시다.
문서 1: 철수는 데이터 과목과 컴구조 과목을 좋아한다.
문서 2: 영이는 컴구조 과목을 싫어한다.
문서 3: 철수는 컴구조 과목을 싫어한다.
(주의 : df-idf 가중치 계산 및 유사도 계산은 내 계산이 틀렸을 수 있음. + 소숫점 반올림-내림 등에 따라 계산 결과 달라질 수 있음.
따라서 계산 원리만 참고하기 바람)
tf
| 문서 / 단어 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 1 | 0 | 1 | 1 | 2 | 1 | 0 |
| 문서 2 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 문서 3 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
위와 같이, 문서 당 등장하는 단어의 빈도수를 벡터로 표시한 것을 tf(= term freqeuncy, 단어빈도수)라고 합니다.
df
| 문서 / 단어 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 통합 문서 | 2 | 1 | 1 | 3 | 3 | 1 | 2 |
또 위와 같이 어떤 단어가 등장하는 문서의 수를 벡터로 표시한 것을 df(=document frequency, 문서빈도수)라고 합니다.
그런데 아까 "어떤 용어 t가 나오는 문서가 희귀할수록, t의 중요도 즉, 정보의 효용도는 커진다"라고 했잖아요. 그럼 df가 커질수록 해당 문서의 중요도가 작아지겠네요?
그래서 문서의 중요도를 반영하기 위해, 다시 용어 t의 역문서 빈도-idf (= inverse document freqency)-라는 것을 정의하게 됩니다.
다음의 식으로 df에서 idf를 계산할 수 있습니다.
df 와 idf

| 문서 / 단어 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 통합 문서 (df) | 2 | 1 | 1 | 3 | 4 | 1 | 2 |
| idf | 0 | 0.18 | 0.18 | -0.12 | -0.22 | 0.18 | 0 |
반올림 전의 idf
| 문서 / 단어 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 통합 문서 (df) | 2 | 1 | 1 | 3 | 4 | 1 | 2 |
| idf | 0 | log(3/2) | log(3/2) | log(3/4) | log(3/5) | log(3/2) | 0 |
반올림 전의 idf(= log형태) 값은 다음과 같다.
df에서 위의 계산식을 적용하면 idf를 구할 수 있습니다. 여기서 N은 문서의 수로, 문서가 문서1, 문서2, 문서3이 있으니 N은 3이 되겠네요. 그럼 여기서 df를 이용해 단어 '영이'의 idf를 구하면, log(3/(1+1))으로, 소수점 셋째자리에서 반 올림하여 약 0.18이 나오게 됩니다.
2) tf-idf 가중치 벡터를 구해볼까요?
tf-idf 가중치
그럼 용어 t의 문서 d에 있어서의 가중치(중요도)는 어떻게 될까요?
여러가지 방법이 있지만, "tf-idf 가중치"라는 방법이 정보 검색 분야에서 가장 많이 사용된다고 해요.
tf가 커지거나 idf가 커질수록 tf-idf 가중치는 증가합니다. 즉, 해당되는 문서에서 용어의 빈도수가 높아지거나 또는 용어가 나오는 문서가 희귀(희소)할수록 가중치가 증가한다는 것이죠.

tf-idf 가중치는 tf 가중치와 idf 가중치를 곱하여 구하므로, 위와 같은 식을 통해 구할 수 있습니다. 앞의 log(1 + tf)는 tf 가중치를 구하는 식, 그리고 뒤의 식은 idf를 구하는 식이죠. 이때, 만일 용어의 빈도수가 0이라면, tf 가중치는 식을 계산하지 않고 0으로 계산한다는 점을 유의합시다.
tf-idf 가중치 벡터
그럼 위의 예시에서의 tf-idf 가중치 벡터를 구해보면 다음과 같이 나옵니다.
| tf-idf 가중치 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | 0.05 | -0.04 | -0.11 | 0.05 | 0 |
| 문서 2 | 0 | 0.05 | 0 | -0.04 | -0.07 | 0 | 0 |
| 문서 3 | 0 | 0 | 0 | -0.04 | -0.07 | 0 | 0 |
반올림 전의 tf-idf 가중치 벡터
| tf-idf 가중치 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | log(2)*log(2/3) | log(2)*log(3/4) | log(3)*log(3/5) | log(2)*log(3/2) | 0 |
| 문서 2 | 0 | log(2)*log(3/2) | 0 | log(2)*log(3/4) | log(2)*log(3/5) | 0 | 0 |
| 문서 3 | 0 | 0 | 0 | log(2)*log(3/4) | log(2)*log(3/5) | 0 | 0 |
반올림 전의 tf-idf 가중치 벡터(= log형태) 값은 다음과 같다.
이때 tf 가중치와 idf 가중치를 곱하는 것이므로, idf가 0이 나온 열 또는 tf 벡터에서 0이 나온 부분을 모두 0으로 채우고 시작하면 더 편합니다. 그 이외의 나머지 부분만 계산하여 채우면 되기 때문입니다.
✍ 코사인 유사도 구하기
3) 아까 구한 가중치 벡터를 바탕으로 '코사인 유사도'를 계산해봅시다.
기존에 질의와 문서에 공통된 용어의 tf-idf 값을 합산하기만 하는 방식은 길이가 긴 문서에 높은 점수를 준다는 단점이 있습니다. 따라서 문서의 길이가 아닌 문서의 내용, 특성만을 기반으로 관련도를 따지려면 코사인 유사도를 사용해야합니다. 문서의 내용(의미)을 결정하는 것은 각 용어의 절대적 빈도수가 아닌, 서로 다른 용어들의 빈도수 분포(비율)이므로 거리 대신 각도를 고려해야하기 때문입니다.

코사인 유사도를 구하려면 우선, 벡터의 크기로 해당 벡터 내부의 각 요소를 나누어주어 정규화시켜야합니다.
| tf-idf 가중치 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | 0.05 | -0.04 | -0.11 | 0.05 | 0 |
| 문서 2 | 0 | 0.05 | 0 | -0.04 | -0.07 | 0 | 0 |
| 문서 3 | 0 | 0 | 0 | -0.04 | -0.07 | 0 | 0 |
여기서 문서 1의 벡터 크기는 다음과 같이 구할 수 있습니다. (반올림하기 전의 나머지 값들은 무시하고 계산합니다)
그러면 약 0.14가 나옵니다.
| tf-idf 가중치 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | 0.05 | -0.04 | -0.11 | 0.05 | 0 |
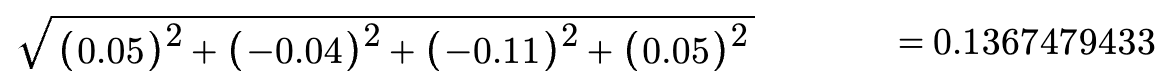
여기 tf-idf 가중치 벡터의 각 요소를 저 벡터 크기인 0.14로 나누어주면 됩니다.
| tf-idf 가중치 | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | 0.05 / 0.14 | -0.04 / 0.14 | -0.11 / 0.14 | 0.05 / 0.14 | 0 |
정규화된 tf-idf 벡터에서, 문서 1에서 '데이터'는 0.05/0.14, 문서 1의 '컴구조'는 -0.04/0.14, 마지막으로 문서 1의 '과목'은 -0.11/0.14로 계산할 수 있습니다. 이런 방식으로 정규화해줍니다.
(반올림 해놓은 값을 이용해 계산하는 등의 오차 요인이 많아, 아래 계산이 틀렸을 수도 있음. 계산법만 숙지하기)
문서 1 뿐만 아니라 문서 2와 문서 3의 벡터도 같은 방식으로 정규화 해줍니다.
정규화된 tf-idf 가중치 벡터
| tf-idf (정규화) | 철수 | 영이 | 데이터 | 컴구조 | 과목 | 좋아 | 싫어 |
| 문서 1 | 0 | 0 | 0.38 | -0.27 | -0.78 | 0.38 | 0 |
| 문서 2 | 0 | 0.56 | 0 | -0.38 | -0.72 | 0 | 0 |
| 문서 3 | 0 | 0 | 0 | -0.47 | -0.87 | 0 | 0 |
정규화 결과, 위와 같은 결과를 얻게 됩니다.
코사인 유사도 계산 & 가장 유사한 문서쌍 찾기
이제 이 정규화된 벡터로, 어떻게 문서들 간의 코사인 유사도를 구할까요?
아주 간답합니다. 가중치 벡터들끼리 내적해주기만 하면 됩니다.
이제 문서들 간의 유사도를 구해볼까요
내적은 간단히 문서1과 문서 2에서 '철수'를 서로 곱한 것 + '' '영이'를 서로 곱한 것 + ... 로 계산할 수 있습니다.

예를 들어, 문서 1과 문서 2의 벡터를 내적할 때는 저렇게 각 요소 별로 곱한 다음에 그 값들을 모두 더해주면 되는 것입니다.
따라서 코사인 유사도는 아래와 같이 계산됩니다.
문서1&문서2 유사도 = 0 + 0 + 0 + (-0.27) * (-0.38) + (-0.78) * (-0.72) + 0 + 0 = 0.6669
문서1&문서3 유사도 = 0.8075
문서2&문서3 유사도 = 0.8097
계산 결과, 문서2~문서3이 유사도 점수가 가장 높았습니다. 즉, 문서 2와 문서 3이 가장 유사하다는 것으로 볼 수 있습니다.
지적이나 피드백, 댓글, 좋아요 전부 환영합니다. 포스팅이 도움이 되었다면 좋아요 눌러주세요~
'IT > 데이터 과학 & 인공지능' 카테고리의 다른 글
| [데이터 사이언스 / R] 결측치와 이상치(극단치)를 처리하는 방법 (예시) (0) | 2022.06.04 |
|---|---|
| [데이터 사이언스 / R] 주성분 분석(PCA), 활용 예시 (feat. k-means 군집화) (0) | 2022.06.03 |
| [데이터 사이언스] R - 숫자가 아닌 값(범주형,명목형)들을 숫자로 변환(매핑) (0) | 2022.04.29 |
| [데이터 사이언스 / R] iris 데이터셋을 이산화. 수치형(연속형) 변수를 명목형 변수로 변환 (0) | 2022.04.08 |
![[데이터 사이언스] 검색 엔진은 어떤 원리로 작동할까? + tf-idf 유사도 예제 풀이](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbJ1rIe%2FbtrFMDShgzQ%2Fl3jDKnt6erTO9kGKDNU5k0%2Fimg.png)