[데이터 사이언스 / R] 주성분 분석(PCA), 활용 예시 (feat. k-means 군집화)

안녕하세요 밥한그릇입니다.

요즘 과제나 배우는 내용이 많아 바쁘다보니, 오히려 포스팅을 자주 못하게 되는 것 같네요.

그러나 공부하던 중 인상깊었던 지식을 공유하고 싶어 포스팅을 씁니다.

 

---

 

R로 데이터 분석을 하다보면, 가장 중요한 과정 중 하나가 변수 선택이죠.

데이터셋에 있는 여러 변수 중 결과에 영향력 있는 변수들만 따로 뽑아, 그걸로 모델을 학습시켜야하니까요.

그렇게 선별한 변수 집합에 서로 다중공선성이 있는 변수들이 포함되거나, 결과와 상관도가 낮은 변수들이 많으면 모델의 성능 및 분석의 정확도가 떨어질 수 있습니다.

그래서 변수의 수는 적게, 성능은 높게 해줄 변수 집합을 찾아야해요.

 

이 과정에서 사용할 수 있는 방법 중 하나가 PCA 분석입니다.

PCA 분석을 통해 차원 축소를 하여, 변수 개수를 줄일 수 있습니다.

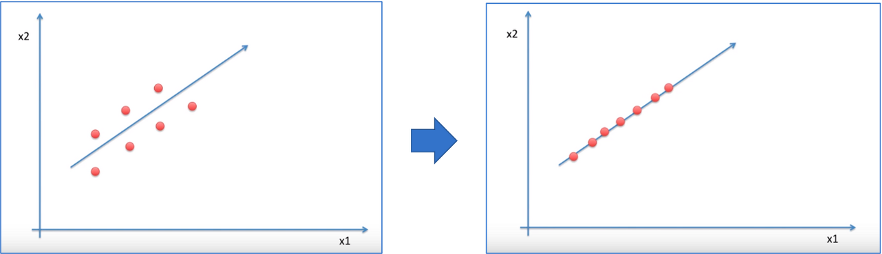
말이 좀 어렵죠? 그냥 변수 여러 개를 합쳐서 새로운 변수들을 구성한다고 보면 됩니다.

 

예를 들면, 변수 3개를 새로운 변수 2개(a, b)로 차원축소 한다고 해봅시다. pca 함수를 돌려보니 변수1은 70%, 변수2는 40% 변수3은 10%를 반영한 새로운 변수 a가 만들어졌다고 쳐봐요. 또 변수1은 60% 변수2는 10%, 변수3을 60% 반영한 새로운 변수 b가 만들어지는 거죠. 예를 들자면 이런 원리입니다. 마치 선형 회귀와도 비슷하네요.

 

그럼 정리해봅시다.

PCA(주성분 분석)이란 무엇인가?

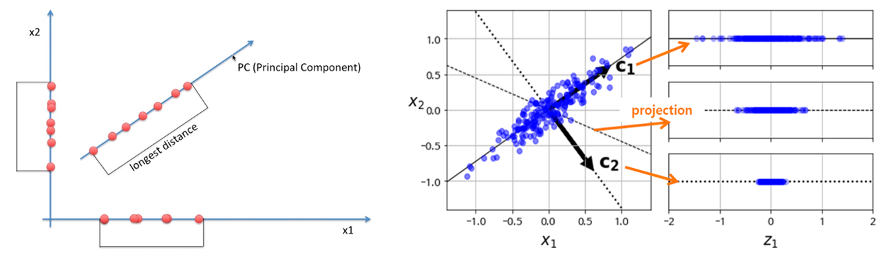
•주성분 분석(PCA)은 기존 변수들의 선형 결합을 이용하여 새로운 축(변수)를 만든다.

•각 주성분 간의 상관계수는 0이기 때문에 주성분 값으로 회귀분석을 진행하게 될 경우, 다중공선성을 걱정하지 않아도 된다

•효과적인 차원축소로 모델을 간단하게 만들 수 있다.

•좌표공간의 수많은 직선 중 가장 분산이 넓은 위치의 직선에 좌표를 사영

사영된 좌표값의 중복을 최소화하여 데이터의 유실을 줄이기 위함이다.

다음은 차원 축소의 원리를 그림으로 나타낸 것입니다. 이 포스팅은 예제 부분이 메인이니, 원리 부분은 자세한 설명을 건너뛸게요.

좌표공간의 수많은 직선 중 가장 분산이 넓은 위치의 직선에 좌표를 사영

좌표공간의 수많은 직선 중 가장 분산이 넓은 위치의 직선에 좌표를 사영

1. 상관계수 분석

변수들 간의 선형 관계가 높지 않으면 굳이 PCA 분석을 할 필요가 없다고 합니다.

따라서 먼저 상관계수 분석이 필요합니다.

일단 제가 고른 데이터셋으로 상관계수 분석을 해본 결과, 대부분 1에 가까운 값으로 선형도가 매우 높게 나왔습니다.

Corr_mat = cor(data)
corrplot(Corr_mat, method = "color", outline = T, addgrid.col = "darkgray", 
        order="hclust", addrect = 4, rect.col = "black", 
        rect.lwd = 5,cl.pos = "b", tl.col = "indianred4", 
        tl.cex = 0.5, cl.cex = 0.5, addCoef.col = "white", 
        number.digits = 2, number.cex = 0.4, 
        col = colorRampPalette(c("darkred","white","midnightblue"))(100))
# 변수들 간의 선형관계가 높음 -> 주성분 분석을 통해 차원 축소 가능.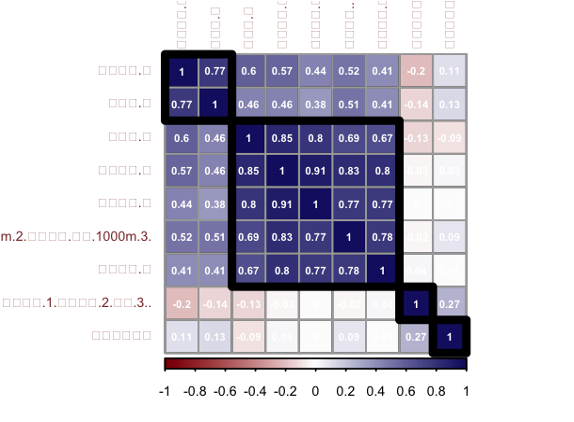

변수들 간의 선형관계 파악

2. PCA 추출, 플롯 출력

주어진 변수를 통해 PCA를 추출했습니다.

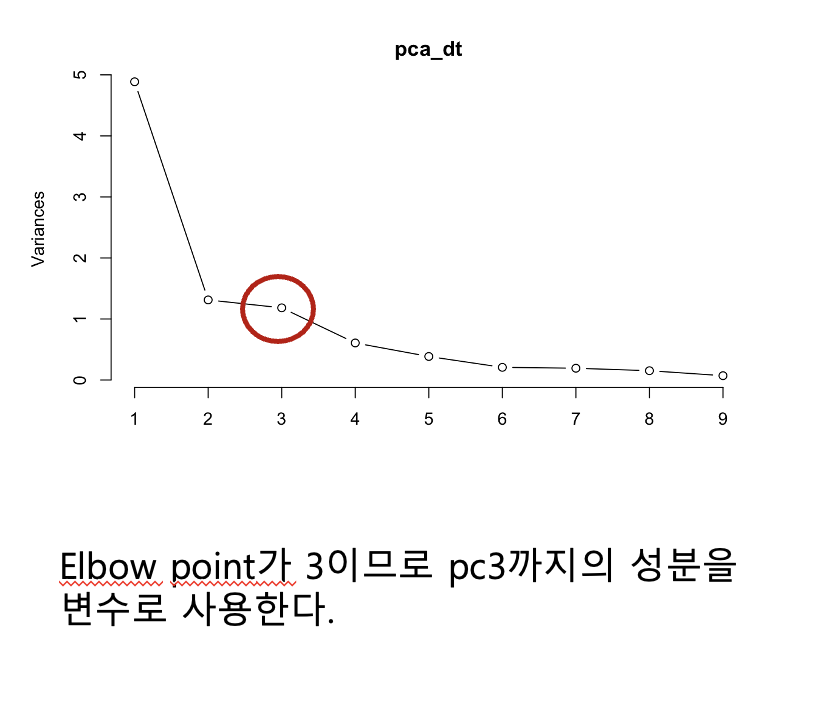
PC3까지가 개별 변동이 13% 이상이고 누적 변동이 82%가 나오는 군요. 그 이후로는 개별 변동이 크지 않아 pc3까지 고르는 것이 적절해보입니다.

또한 pca를 플롯하였을 때 elbow point도 3이 나와 PC1부터 PC3까지의 변수만 사용하기로 했습니다.

(참고로 elbow point는 그래프의 기울기가 갑자기 변하는 지점. 팔꿈치와도 같다고 하여 저렇게 부른다.)

# 데이터에서 주성분을 추출하여 변수를 축소하기 위한 기법이 바로 PCA
pca_dt <- prcomp(data,scale.unit = TRUE, graph = FALSE)
pca_dt
plot(pca_dt, type = "l") # elbow point = 3
summary(pca_dt) # PC3까지만 변수를 사용해도 데이터의 약 82%만큼의 변동을 설명할 수 있음

 

3. PCA 성분 선택

앞서 PCA 성분 중 pc1~pc3을 선택하는 것이 좋다고 결론 내렸으므로, 그렇게 합니다.

새롭게 변수를 구성했으므로, 이를 Plot 하여 데이터의 분포를 살펴보면 다음과 같습니다.

# First for principal components
comp <- data.frame(pca_dt$x[,1:3])
# Plot
plot(comp, pch=16, col=rgb(0,0,0,0.5))

 

4. PCA 성분으로 K-means 군집화 수행 - PCA 수행하지 않은 경우와 비교

군집화를 수행하여 그 성능을 비교하면 다음과 같습니다.

k-means 군집화는 거리기반 알고리즘이라 고차원에서 성능이 떨어지기 쉬우므로, 차원축소 시 성능 향상에 매우 효과적입니다.

set.seed(1234)
# 일반 변수들을 모두 포함한 군집화 수행 결과 
k_var <- kmeans(data, 3, iter.max=1000)
palette(alpha(brewer.pal(9,'Set1'), 0.5))
plot(data, col=k_var$clust, pch=16)
k_var # (between_SS / total_SS =  46.8 %)

# pca를 통한 군집화 수행 결과
k_pca <- kmeans(comp, 3, iter.max=1000)
palette(alpha(brewer.pal(9,'Set1'), 0.5))
plot(comp, col=k_pca$clust, pch=16)
k_pca # (between_SS / total_SS =  56.3 %))

 

5. PCA로 군집화한 결과의 의미 분석

모델의 성능(정확도)이 좋다고 해도, 그 의미를 모르면 무용지물이겠죠. 결과물이 어떤 의미를 가지는 지 알아야 합니다.

이때 의미에 대한 분석은 먼저 각 변수가 어떤 의미를 가지는 지 알아야 가능해요.

 

다음은 그전 군집화 모델에서 약간의 최적화를 더 수행하여 나온 모델(성능 약 60.6%)의 결과입니다. 군집의 중심점을 기준으로 군집화 결과를 분석하였습니다.

 

저는 다음과 같은 단계를 통해 임의로 의미를 분석해보았습니다.

 

a) 군집의 중심점과 각 변수의 분포 범위를 사용해서 군집의 대략적인 위치를 파악합니다.

b) 그 분포 범위를 각 성분에 적용해서 그 성분의 의미를 찾습니다.

c) 임의로 그 성분에 대한 이름을 지어주고, b번의 결과에 적용합니다.

d) c번을 이용해 데이터에 대한 분석(결론)을 도출합니다. 

pca 성분의 방향성

(a) 군집의 중심점과 각 변수의 분포 범위를 사용해서 군집의 위치를 파악

(b) 그 분포 범위를 각 성분에 적용 + 그 성분의 의미를 찾기 (높다, 보통, 낮다 등) / (c) 임의로 그 성분에 대한 이름을 지어주고, b번의 결과에 적용

(d) c번을 이용해 데이터에 대한 분석(결론)을 도출